Python
QuadTree


return to main index

Downloads:
    quadtree.zip



Introduction

A quadtree is a data structure that stores information about a surface after it has been sub-divided into rectangles. The rectangles differ in size but the smallest are those that are considered imporatnt because they cross or contain a feature of some kind. The information about each rectangle is stored in a unit of data called a node. For example, figure 1 shows a simple subdivision in which the smallest rectangles are those that intersect the circumference of a circle.



Figure 1


A node stores the coordinates of the vertices a rectangle as well as a reference to the parent node of which it is a subdivision. Some nodes also store references to children nodes - rectangles within rectangless. There are three types of node:


  • ROOT node: represents the original undivided surface,
  • BRANCH node: represents a subdivision,
  • LEAF node: represents a minimum size rectangle that interects a feature.

A root node of a has up to four children nodes but it does not have a parent node because it represents the original surface. Branch nodes have a parent node and may also have up to four children nodes. Leaf nodes have a parent node but no children nodes because they represent the minimum size subdivision.

The data in a quadtree is accumulated as a result of subdividing the original surface in a repetitive fashion. The process is recursive; the original surface is subdivided into four sub-rectangles each of which is likewise subdivided. Subdivision only occurs if a rectangle spans a feature such as a circle shown in figure 1. The process terminates when a rectangle reaches a minimum size. The order in which rectangles are subdivided are shown in figure 2.



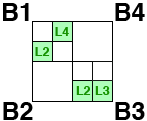
Figure 2


Quadtrees are represented as an inverted tree - the root node at the top and the leaf nodes at the bottom. An illustration of a simple quadtree is shown in figure 3. Such diagrams are called graphs. 

                                     Root                         
                                      |                    depth: 0  
                   ------------|------------------------|  
                   |                       |          
                   B1                      B3              depth: 1  
             |-----|---|---          |------------| 
                |         |              |    |
                L2        L4             L2   L3           depth: 2

Figure 3


The repetitive nature of the 1/2/3/4 recursive subdivision is clearly shown by the animation linked to figure 1.


Base & Derived Classes

Listing 1 implements two base classes that can be extended for the purpose of experimenting with a quadtree. Save listing 1 as quadtree.py. Listing 2 provides a example of super-classing the Node and QuadTree classes to implement a quadtree whose leaf nodes span the circumferences of an arbitary number of circles. Save listing 2 as cquadtree.py.

To visualize the data in the quadtree the vertices of its nodes are used to generate an archive rib file containing a list of RenderMan Polygon statements. The height (y axis) of each polygon is determined by the "recursion depth" of the node that it represents - figures 4 and 5.



Figure 4



Figure 5


Listing 1 (quadtree.py)

# quadtree.py
# Implements a Node and QuadTree class that can be used as 
# base classes for more sophisticated implementations.
# Malcolm Kesson Dec 19 2012
class Node():
    ROOT = 0
    BRANCH = 1
    LEAF = 2
    minsize = 1   # Set by QuadTree
    #_______________________________________________________
    # In the case of a root node "parent" will be None. The
    # "rect" lists the minx,minz,maxx,maxz of the rectangle
    # represented by the node.
    def __init__(self, parent, rect):
        self.parent = parent
        self.children = [None,None,None,None]
        if parent == None:
            self.depth = 0
        else:
            self.depth = parent.depth + 1
        self.rect = rect
        x0,z0,x1,z1 = rect
        if self.parent == None:
            self.type = Node.ROOT
        elif (x1 - x0) <= Node.minsize:
            self.type = Node.LEAF
        else:
            self.type = Node.BRANCH
    #_______________________________________________________
    # Recursively subdivides a rectangle. Division occurs 
    # ONLY if the rectangle spans a "feature of interest".
    def subdivide(self):
        if self.type == Node.LEAF:
            return
        x0,z0,x1,z1 = self.rect
        h = (x1 - x0)/2
        rects = []
        rects.append( (x0, z0, x0 + h, z0 + h) )
        rects.append( (x0, z0 + h, x0 + h, z1) )
        rects.append( (x0 + h, z0 + h, x1, z1) )
        rects.append( (x0 + h, z0, x1, z0 + h) )
        for n in range(len(rects)):
            span = self.spans_feature(rects[n])
            if span == True:
                self.children[n] = self.getinstance(rects[n])
                self.children[n].subdivide() # << recursion
    #_______________________________________________________
    # A utility proc that returns True if the coordinates of
    # a point are within the bounding box of the node.
    def contains(self, x, z):
        x0,z0,x1,z1 = self.rect
        if x >= x0 and x <= x1 and z >= z0 and z <= z1:
            return True
        return False
    #_______________________________________________________
    # Sub-classes must override these two methods.
    def getinstance(self,rect):
        return Node(self,rect)            
    def spans_feature(self, rect):
        return False
  
#===========================================================            
class QuadTree():
    maxdepth = 1 # the "depth" of the tree
    leaves = []
    allnodes = []
    #_______________________________________________________
    def __init__(self, rootnode, minrect):
        Node.minsize = minrect
        rootnode.subdivide() # constructs the network of nodes
        self.prune(rootnode)
        self.traverse(rootnode)
    #_______________________________________________________
    # Sets children of 'node' to None if they do not have any
    # LEAF nodes.        
    def prune(self, node):
        if node.type == Node.LEAF:
            return 1
        leafcount = 0
        removals = []
        for child in node.children:
            if child != None:
                leafcount += self.prune(child)
                if leafcount == 0:
                    removals.append(child)
        for item in removals:
            n = node.children.index(item)
            node.children[n] = None        
        return leafcount
    #_______________________________________________________
    # Appends all nodes to a "generic" list, but only LEAF 
    # nodes are appended to the list of leaves.
    def traverse(self, node):
        QuadTree.allnodes.append(node)
        if node.type == Node.LEAF:
            QuadTree.leaves.append(node)
            if node.depth > QuadTree.maxdepth:
                QuadTree.maxdepth = node.depth
        for child in node.children:
            if child != None:
                self.traverse(child) # << recursion

Listing 2 (cquadtree.py)

# cquadtree.py
# A relatively simple example of using the Node and QuadTree 
# class.
# Malcolm Kesson Dec 19 2012
from quadtree import Node, QuadTree
from distances import pnt2line
import random
  
#____UTILITY PROCS_______________________________________
# Returns the length of a vector "connecting" p0 to p1.
# To avoid using the sqrt() function the return value is
# the length squared.
def dist_sqrd(p0, p1):
    x,y,z = p0
    X,Y,Z = p1
    i,j,k = (X - x, Y - y, Z - z)
    return i * i + j * j + k * k
#_______________________________________________________
def getedges(rect):
    x0,z0,x1,z1 = rect
    edges = ( ((x0,0,z0),(x1,0,z0)), # top
              ((x1,0,z0),(x1,0,z1)), # right
              ((x1,0,z1),(x0,0,z1)), # bottom
              ((x0,0,z1),(x0,0,z0))) # left
    return edges
#_______________________________________________________
  
class CNode(Node):
    #_______________________________________________________
    # Overrides the base class method.
    # Ensures Node.subdivide() uses instances of our custom 
    # class rather than instances of the base 'Node' class.
    def getinstance(self,rect):
        return CNode(self,rect)
    
    #_______________________________________________________
    # Overrides the base class method.
    # Test if the vertices of a rectangle spans the circumference 
    # of a circle(s). To avoid sampling errors the proc returns True
    # if any edge lies within the radius of any circle. However, the
    # 'edge test' is applied only to rectangles whose parent node has
    # a depth of recursion less than a specific (arbitary) value.
    def spans_feature(self, rect):
        x0,z0,x1,z1 = rect
        if self.depth < 3: # this may require adjustment
            for circle in CQuadTree.circles:
                rad,x,y,z = circle
                edges = getedges(rect)
                for edge in edges:
                    dist,loc = pnt2line( (x,0,z), edge[0], edge[1] )
                    if dist <= rad:
                        return True
        verts = [(x0,0,z0),(x0,0,z1),(x1,0,z1),(x1,0,z0)]
        for circle in CQuadTree.circles:
            rad,x,y,z = circle
            rad_sqrd = rad * rad
            center = (x,y,z)
            span = 0
            for vert in verts:
                d = dist_sqrd(vert,center)
                span += (d <= rad_sqrd)
            if span > 0 and span < 4:
                return True
        return False
         
class CQuadTree(QuadTree):
    circles = []   # list of tuples (rad,x,y,z)
    #_______________________________________________________
    def __init__(self, rootnode, minrect, circles):
        CQuadTree.circles = circles
        QuadTree.__init__(self, rootnode, minrect)
        
#_______________________________________________________
# Returns a string containing the rib statement for a
# four sided polygon positioned at height "y".
def RiPolygon(rect, y):    
    x0,z0,x1,z1 = rect
    verts = []
    verts.append(' %1.3f %1.3f %1.3f' % (x0,y,z0))
    verts.append(' %1.3f %1.3f %1.3f' % (x0,y,z1))
    verts.append(' %1.3f %1.3f %1.3f' % (x1,y,z1))
    verts.append(' %1.3f %1.3f %1.3f' % (x1,y,z0))
    rib =  '\tPolygon "P" ['
    rib += ''.join(verts)
    rib += ']\n'
    return rib
#_______________________________________________________
  
if __name__=="__main__":
    rootrect = [-2.0, -2.0, 2.0, 2.0]
    resolution = 0.02
  
    circles = []
    random.seed(1)
    for n in range(17):
        r = random.uniform(0.2, 0.8)
        x = random.uniform(-2.0, 2.0)
        z = random.uniform(-2.0, 2.0)
        circles.append( (r,x,0,z) )
        
    #circles = [(1.9,0,0,0),(1.0,0.95,0,0)]
    rootnode = CNode(None, rootrect)
    tree = CQuadTree(rootnode, resolution, circles)
    
    # Output RenderMan polygons for each node
    ribpath = '/Users/mkesson/leaves.rib'
    f = open(ribpath,'w')
    f.write('AttributeBegin\n')
    for node in CQuadTree.allnodes:
        height = node.depth * 0.1
        if node.depth == CQuadTree.maxdepth:
            f.write('\tColor 0 .5 0\n')
        else:
            f.write('\tColor 1 1 1\n')
        f.write(RiPolygon(node.rect, height))
    f.write('AttributeEnd\n')
    f.close()
    print('Wrote %d polygons' % len(CQuadTree.leaves))



© 2002- Malcolm Kesson. All rights reserved.