Reference
Expressions

return to main index

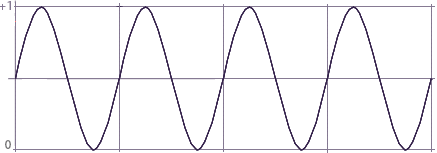
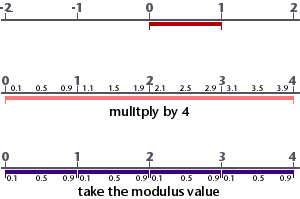
Introduction

This page presents a collection of expressions that can be used with source code for surface and displacement shaders. The expressions use the values of the global variables s and t, both of which by default are in the range 0 to 1, to calculate values in other ranges.

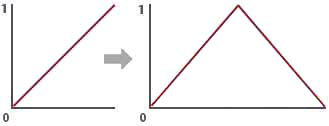
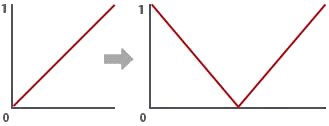
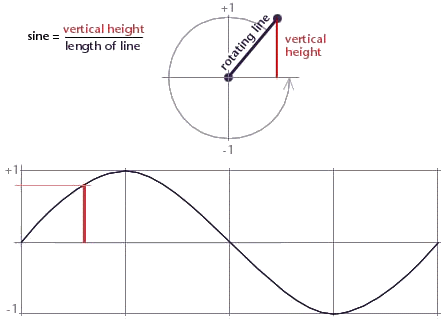
Figure 1

Being able to conveniently convert one range of values into another range is very useful when, for example, the effect of a surface or displacement shader needs to be gradually modified towards the edges of a surface.

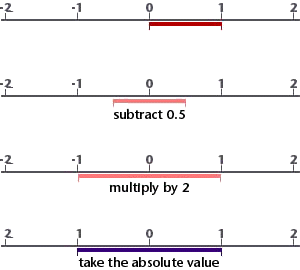
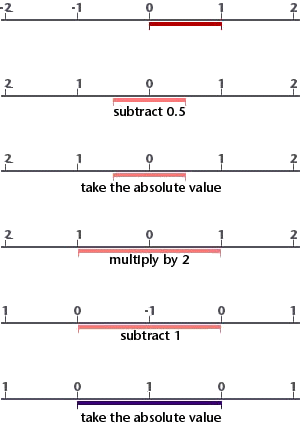
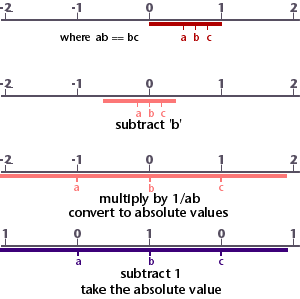
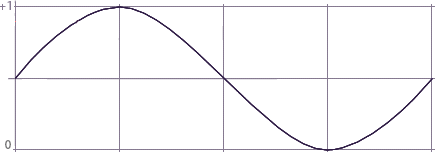
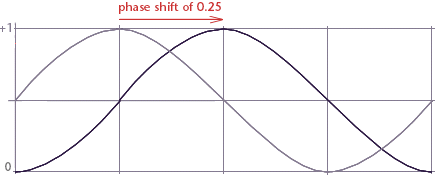
Figure 2

Mapping 0 - 1 to 1 - 0 - 1

Deriving an expression that will convert values in one range to their associated values in another range can be visualized as a process of 'moving' and 'stretching' the initial range, say 0 to 1, along a fixed number line.

Figure 3

For example, the diagram below shows the original range, 0 to 1, being mapped to the range 1 to 0 to 1.

Figure 4

If the original range of values was represened by say the s texture coordinate, new values could be calculated using the following expression.
    newValue = abs((s - 0.5) * 2);

The effect of using newValue to scale the displacement of a wave is shown below.

Figure 5

Mapping 0 - 1 to 0 - 1 - 0

The diagram below shows the original range, 0 to 1, being mapped to the range 0 to 1 to 0.

Figure 6

The equivalent expression is,
    newValue = abs (abs(s - 0.5) * 2 - 1);

The effect of using newValue, calculated with both 's' and 't', to scale the displacement of a turbulance shader is shown below.

Figure 7

Mapping a Subrange to 0 - 1 - 0

The diagrams show a subrange a to c being mapped to the range 0 to 1 to 0. It is assumed b is the midpoint of ac

Figure 8

Figure 9

The equivalent expression is,
    newValue = abs (abs((s - b) * 1/ab) - 1);

The effect of using this expression to calculate a displacement in both 's' and 't' is shown below.

Figure 10

Using the Sine Function

The sine function is part of the maths library that is built into the shading language. The function returns a value that is the ratio of the length of a rotating line divided by its vertical height. The end of the rotating line sweeps out the circumference of a circle. If the line is one unit long the circumference of the circle is 2 x PI or 6.283185 units in length.

Figure 11

In the diagram shown above the vertical height of the rotating line, itself 1 unit in length, can never be greater than +1 and never be less than -1. Consequently for any rotation of the line, measured by the distance its end has moved along the circumference of the circle, the sine function returns values in the range +1 to -1. The unit of measurement used to express the rotation is the radian.

To generate the sine wave shown above across a surface, say in the 's' direction, we must scale its value by 2PI ie. multiply by 6.283185.
    waveHeight = sin (s * 6.283185);

The effect of using waveHeight in a displacement shader is shown below.

Figure 12

To avoid negative numbers it is often necessary to keep waveHeight in the range 0 to 1. The following expression accomplishes this,
    waveHeight = (sin(s * 6.283185) + 1) * 0.5;

Figure 13

It is also useful to be able to shift the sine wave horizonally so that the wave begins and ends at a 'trough', a 'peak' or anywhere in between. The following expression introduces control over the phase of the wave.
    waveHeight = (sin ((s - phase) * 6.283185) + 1.0) * 0.5;
when "phase" is 1.0 the wave is shifted one complete cycle.

Figure 14

Often an arbitary number of cycles of the sine wave is required, the following expression includes a variable that controls the number of waves,
    waveHeight = (sin((s-phase/cycles)*6.283185*cycles) + 1.0)*0.5;

Figure 15

The effect of using this expression in a displacement shader is shown below.

Figure 16

Occasionally it is necessary to modify the sine wave so that it produces only 'bumps'. Here is the expression,
    waveHeight = abs (sin ((s - phase/cycles) * 6.282 * cycles));
Used in a displacement shader this expression produces the effect shown below.

Figure 17

Using the Mod Function

The mod function divides one number by another but returns only the remainder. For example,
    mod (3, 2);
would return the value 0.5, not 1.5.
The function can be used to map the range 0 to 1 to a sequence of repeating sub-ranges 0 to ~1. In each sub-range the maximum value becomes infinitly close to 1 but never actually reaches that value.

Figure 18

The mod function is very useful when creating repeating patterns on a surface. In the diagram above, 4 sub-ranges have been created, however, the function can be used to make any number of repeats. To generate 8 repeated patterns, say in the 's' direction, the following expression would be applied.
    ss = mod (s * 8, 1);
Using 1 as the divider ensures the number of 'repeats' is not altered. The effect of using mod in a displacement shader, in both the 's' and 't' directions is shown below.

Figure 19