Mel
Modeling with Smart Transforms

return to main index

Introduction

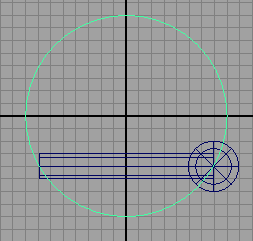
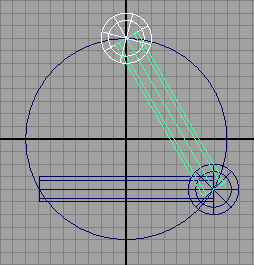
The mel script in listing 1 produces a ring-like structure built from a repetition of spheres and cylinders - figure 1. This tutorial demonstrates how repetitive modeling can be accomplished using instancing and smart transforms.

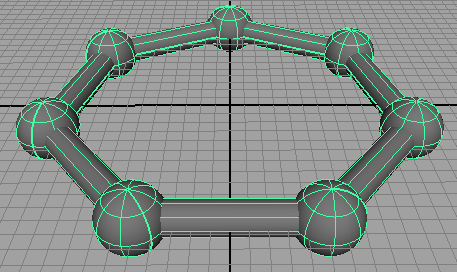
Figure 1

Basic Code

Listing 1 provides the code for a procedure that can model a ring consisting of cylinders and spheres. Given the number of radius of the ring ($R) and the number of sides ($nsides) the procedure calculates the angle between the cylinders and their lengths.

Listing 1 (ring.mel)

global proc string ring(int  $nsides, float  $R)
{
// Give the number of sides and the radius of the "ring"
// calculate its proportions                                    
float $theta = 360.0/$nsides;
float $rads = deg_to_rad($theta/2);
float $A = $R * cos($rads);
float $B = $R * sin($rads);
float $ratio = (2 * $B)/0.5;   // cylinder height ratio
 
// The "ring consists of repeated cylinders and spheres  
string $c[] = `cylinder -p 0 0 $A -r .5 -ax 1 0 0 -hr $ratio`;
string $s[] = `sphere -p $B 0 $A -ax 0 1 0`;
select $s[0] $c[0];
  
// Use either duplication or instancing
//string $d[] = `duplicate -rr`;
string $d[] = `instance`;
rotate -r 0 $theta 0;
  
// Begin making a array (ie. list) of the items that will
// form the "ring" group
string $names[] = { $s[0], $c[0] };
appendStringArray($names, $d, size($d));
  
int $n = 2;
for($i = 2; $i < $nsides; $i++)
    {
    // Use either duplication or instancing
    //$d[] = `duplicate -rr -st`;
    $d = `instance -st`;
    appendStringArray($names, $d, size($d));
    }
// Handy for printing the contents of the group 
//for($i = 0; $i < size($names); $i++)
//      print($names[$i] + "\n");
return `group $names`;
}

Calculating the Sides

The calculation of the angle and the length of each cylinder proceeds as follows.

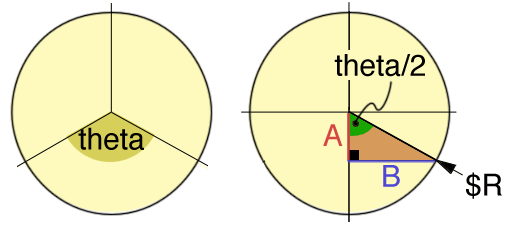
Figures 2 & 3

For the purpose of explaining how the angle and length of each cylinder in the "ring" is calculated assume the perimeter of the circle in figure 2 is to be divided into three segments. The angle theta can be found by dividing 360 degrees by the number of sides. Since sides A and B form a right-angled triangle, with the radius of the circle ($R) as the hypotenuse, their lengths can be found using trigonometry.

Irrespective of the size of a right-angled triangle, dividing side A by the hypotenuse ($R) yields a ratio that is constant for the included angle (theta/2) ie. the sine of the angle.

    A/$R = sin(theta/2);

Since theta is known, side A can be calculated as,

    A = $R * sin(theta/2);

Because the trigonometry procedures in mel measure angles in radians, not degrees, the angle, theta/2, is converted to radians prior to being used by sin() and cos().

Figure 3

Figure 4

Figure 3 shows the result of executing lines 1 to 14 of the procedure ring(). The remaining code simply "clones" the original sphere and cylinder using instance() followed by a transformation that rotates the "clone" into its first position. The smart transform flag -st ensures the "clones" use the same transformations as the master object from which they were instanced. The ring() procedure concludes by grouping the surfaces and returning the name of the group.