Introduction
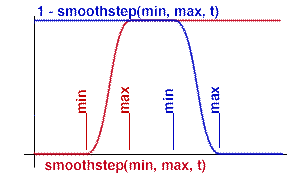
The function smoothstep() is part of the maths library of shading language
functions. Given three values, min, max and input, the
function will return a number between 0 and 1 that represents the relationship
of the input value to the min and max values.
If input is less than min, smoothstep() will return 0.
If input is equal to, or larger than max, smoothstep() will return 1.
If input is between min and max, smoothstep() will return
a value (proportionately) between 0 and 1.0.
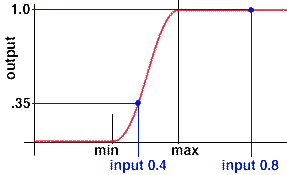
For example, suppose the min and max values are 0.3 and 0.6. Using
the smoothstep function with input values of 0.4 and 0.8 we get
output values of 0.35 and 1.0.
smoothstep(0.3, 0.6, 0.4); smoothstep(0.3, 0.6, 0.8);