Vector Length
Figure 1 shows a fixed vector with the following
coordinates ie. components,
a[3 1 2]
in other words,
ax = 3,
ay = 1,
az = 2,
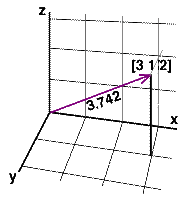
Figure 1
The magnitude (length) of the vector is,
length = sqrt((ax * ax) + (ay * ay) + (az * az))
length = sqrt(9 + 1 + 4) = 3.742
As a short-hand notation the magnitude of a vector is written with two vertical lines,
|a|= sqrt((ax * ax) + (ay * ay) + (az * az))